Constraint Programming Using Choco

1. Overview

In this tutorial, we’ll learn about Choco-solver, a popular Java Constraint Programming (CP) framework.

Overall, we’ll briefly understand the fundamentals of CP and then look at the key concepts of the Choco-solver library. Finally, we’ll create a small program using the library to solve sudoku puzzles.

2. Constraint Programming Concept

CP is a paradigm different from traditional deterministic or imperative programming that helps solve combinatorial problems. A few use cases related to constraint programming include scheduling, planning, routing, packing, resource allocation, and solving sudoku puzzles.

First, let’s go over the main constructs of CP:

• Variables: A group of unknowns X₁, X₂, X₃,…, X_n
• Domain: Possible values of the unknowns, represented as D₁, D₂, D₃,…, D_k
• Constraints: Rules or criteria that should be satisfied when the domain values are assigned to the variables, represented as C₁, C₂, C₃,…, Cm
• Often represented as P = (X, D, C), where P stands for Problem

3. Prerequisite

Before we can start using Choco-solver, let’s import the necessary Maven dependency:

<dependency>
   <groupId>org.choco-solver</groupId>
   <artifactId>choco-solver</artifactId>
   <version>4.10.14</version>
</dependency>

4. Key Components of Choco-solver

Let’s examine the key components of the Choco-solver framework. In the library, the Model class is the container or the context that holds the variables and constraints:

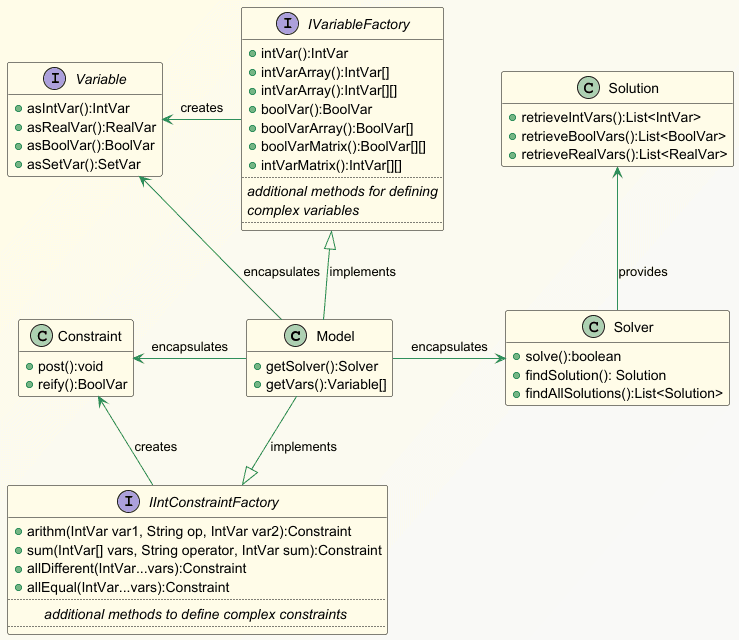
The Variable and Constraint classes represent the variables and constraints in the CP programming paradigm. The Model class implements the IVariableFactory interface including methods defining the variables and their domain values efficiently. Moreover, its ability to create single and multi-dimensional arrays of domain values provides excellent flexibility and convenience to model complex problems.

In addition, the Model class implements constraint factory interfaces like IIntConstraintFactory. Hence, its methods such as arithm(), sum(), allDifferent(), etc. help define arithmetic relationships between the variables. The library provides numerous other methods to set up more complex constraints.

After defining the variables and the constraints, we can call the Model#getSolver() method to get the Solver class. Further, its methods like Solver#solve() and Solver#findSolution() help get the solution.

Moreover, this article is just a preview of the broader capabilities of the Choco-solver library. It provides the impetus to explore the library’s more complex functionalities.

In the next section, we’ll learn more when we implement the solution for a sudoku board.

5. Solve a Blank Sudoku Board

A sudoku board is a 9 x 9 matrix with nine 3 x 3 matrices with unique values between 1 and 9.

The blank sudoku board can have multiple solutions. We’ll represent each cell as a variable with domain values from 1 to 9 and implement a SudokuSolver class using the Choco-solver library.

5.1. Find Multiple Solutions

Let’s look at the SudokuSolver#findSolutions() method:

List<Integer[][]> findSolutions(final int MAX_SOLUTIONS) {
    IntVar[][] sudokuCells = createModelAndVariables();
    setConstraints(sudokuCells);
    List<Integer[][]> solvedSudokuBoards = getSolutions(MAX_SOLUTIONS);
    return solvedSudokuBoards;
}

It creates a model and its variables in sudokuCells. Then, it sets the constraints on the variables and finally gets the solutions.

5.2. Create Model and Variables

The createModelAndVariables() method instantiates the Model and returns a 9 x 9 matrix:

IntVar[][] createModelAndVariables() {
    sudokuModel = new Model("Sudoku Solver");
    IntVar[][] sudokuCells = sudokuModel.intVarMatrix("board", 9, 9, 1, 9);
    return sudokuCells;
}

First, we create the Model object with the identifier Sudoku Solver. Next, we create a two-dimensional 9 x 9 matrix by calling Model#intVarMatrix() on the newly created Model object. It contains IntVar variables with domain values ranging from  1 to 9.

5.3. Set Constraints on Variables

In the next step, we set the constraint on the Model object’s domain variables:

void setConstraints(IntVar[][] sudokuCells) {
    for (int i = 0; i < 9; i++) {
        IntVar[] rowCells = getRowCells(sudokuCells, i);
        sudokuModel.allDifferent(rowCells).post();
        IntVar[] columnCells = getColumnCells(sudokuCells, i);
        sudokuModel.allDifferent(columnCells).post();
    }
    for (int i = 0; i < 9; i += 3) {
        for (int j = 0; j < 9; j += 3) {
            IntVar[] cellsInRange = getCellsInRange(j, j + 2, i, i + 2, sudokuCells);
            sudokuModel.allDifferent(cellsInRange).post();
        }
    }
}

The getRowCells() and getColumnCells() methods return all cells in the i^th row and column, respectively. Then, Model#allDifferent() sets constraints on the retrieved cell variables in each of the nine rows and columns of the sudoku board. It ensures that domain values 1-9 don’t repeat in any row or column.

Additionally, we retrieve the cells of all the 3 x 3 grids and apply constraints to ensure unique values in their cells.

5.4. Get Solutions

Finally, after setting the constraint, we call the getSolutions() method:

List<Integer[][]> getSolutions(int MAX_SOLUTIONS) {
    List<Integer[][]> solvedSudokuBoards = new ArrayList<>();
    int solutionCount = 0;
    while (sudokuModel.getSolver().solve()) {
        if (solutionCount++ > MAX_SOLUTIONS - 1) {
            break;
        }
        IntVar[] solvedSudokuCells = sudokuModel.retrieveIntVars(true);
        solvedSudokuBoards.add(getNineByNineMatrix(solvedSudokuCells));
        sudokuModel.getSolver().reset();
    }
    return solvedSudokuBoards;
}

The method returns multiple two-dimensional arrays containing the solution in a List. Model#getSolver() gets the Solver object, on which we call Solver#solve() to populate the IntVar variables in the Model with the solution.

Later, we retrieve all the cell values in an array by calling Model#retrieveIntVars(). At the end of the loop, we call Solver#reset() to reset the variable values. Subsequently, the library populates a new solution into the variables in the following iteration.

5.5. Results

Now, lets run the SudokuSolver#findSolutions() method to check the result:

void whenSudokuBoardIsEmpty_thenFindTwoSolutions() {
    SudokuSolver sudokuSolver = new SudokuSolver();
    List<Integer[][]> sudokuSolutionMatrices = sudokuSolver.findSolutions(2);
    sudokuSolutionMatrices.forEach(e -> checkValidity(e));
    sudokuSolutionMatrices.forEach(sudokuSolver::printSolution);
}

The program helps find two possible solutions for a blank sudoku board. After finding the solutions, it calls checkValidity() to validate the results. Finally, the SudokuSolver#printSolution() method prints the 9 x 9 sudoku board:

3 7 2 | 1 5 6 | 4 9 8 
8 4 5 | 2 3 9 | 6 7 1 
1 9 6 | 8 7 4 | 3 2 5 
---------------------
5 3 1 | 6 2 7 | 8 4 9 
4 2 9 | 3 8 5 | 7 1 6 
7 6 8 | 4 9 1 | 2 5 3 
---------------------
9 1 4 | 7 6 3 | 5 8 2 
6 8 7 | 5 1 2 | 9 3 4 
2 5 3 | 9 4 8 | 1 6 7 

Similarly, multiple solutions can be retrieved and printed.

6. Solve a Partially Solved Sudoku Board

Usually, in sudoku puzzles, the board is partially filled. This time we’ll approach the problem similarly to the previous section. However, there’ll be a single solution.

6.1. Find Single Solution

For such a scenario, let’s implement the findSolution() method in the SudokuSolver class:

Integer[][] findSolution(int[][] preSolvedSudokuMatrix) {
    IntVar[][] sudokuCells = createModelAndVariables();
    setConstraints(sudokuCells, preSolvedSudokuMatrix);
    Solution solution = sudokuModel.getSolver().findSolution();
    IntVar[] solvedSudokuCells = solution.retrieveIntVars(true).toArray(new IntVar[0]);
    return getNineByNineMatrix(solvedSudokuCells);
}

The program declares the variables and sets the constraint like before. However, unlike the previous example, it calls an overloaded setConstraints() method with an additional two-dimensional array argument. The unresolved cells are represented with a value of 0 in the two-dimensional preSolvedSudokuMatrix array.

Let’s now look at the method setConstraints():

void setConstraints(IntVar[][] sudokuCells, int[][] preSolvedSudokuMatrix) {
    setConstraints(sudokuCells);
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            if (preSolvedSudokuMatrix[i][j] != 0) {
                sudokuCells[i][j].eq(preSolvedSudokuMatrix[i][j])
                  .post();
            }
        }
    }
}

First, the call to setConstraints() helps set the default constraints like before. Then, the eq() method inherited from the ArExpression interface, applies constraint to assign the prepopulated cell values from preSolvedSudokuMatrix.

Finally, in the SudokuSolver#findSolution() method we call Solver#findSolution() to get the Solution object. Eventually, Solution#retrieveIntVars() helps retrieve the populated cells.

6.2. Results

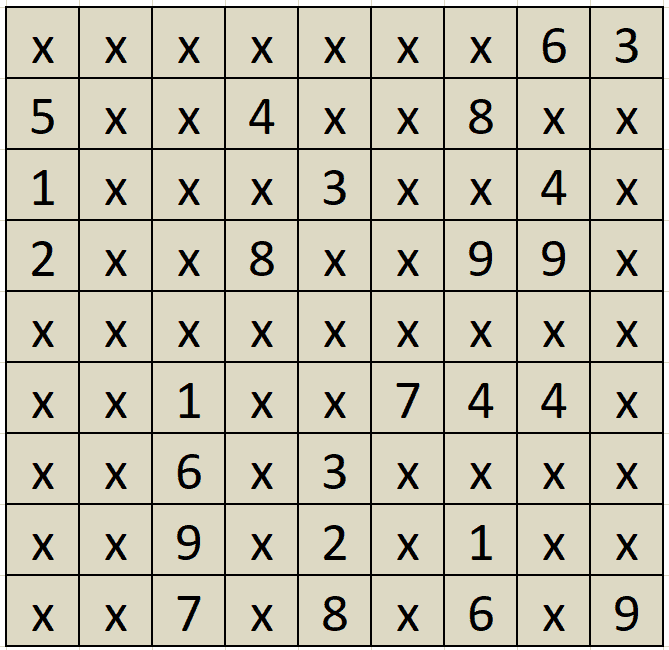
Let’s consider a prefilled sudoku board:

Let’s run the SudokuSolver#findSolution() method to populate the rest of the fields:

void whenSudokuPartiallySolved_thenFindSolution() {
    SudokuSolver sudokuSolver = new SudokuSolver();
    Integer[][] solvedSudokuBoard = sudokuSolver.findSolution(initialValues);
    checkValidity(solvedSudokuBoard);
    sudokuSolver.printSolution(solvedSudokuBoard);
}

We validate the results from SudokuSolver#findSolution() using the checkValidity() method. Thereafter, we print the solution:

9 8 4 | 7 5 1 | 2 6 3 
5 7 3 | 4 6 2 | 8 9 1 
1 6 2 | 9 3 8 | 5 4 7 
---------------------
2 4 5 | 8 1 3 | 9 7 6 
7 9 8 | 6 2 4 | 3 1 5 
6 3 1 | 5 9 7 | 4 2 8 
---------------------
8 1 6 | 3 4 9 | 7 5 2 
3 5 9 | 2 7 6 | 1 8 4 
4 2 7 | 1 8 5 | 6 3 9

7. Conclusion

In this article, we explored Choco-solver, a versatile and expressive open-source library for solving combinatorial problems.

The library helps model the problem almost declaratively by defining the variables, their domain values, and constraints. Therefore, it allows us to obtain multiple solutions without writing any domain-specific logic.

As usual, the source code used in this article can be referred over on GitHub.